(Download full document here.)
Contents
The MTI and RMTI as tools for unmasking the fishing down phenomenon
Background
Region-based Marine Trophic Index (RMTI)
Conceptualization and definition of RMTI
Defining the original MTI and FiB
Detection of expansion in fisheries
Estimation of Region-based MTIs (RMTI)
Example of RMTI application: India
Conclusion
The MTI and RMTI as tools for unmasking the fishing down phenomenon
Kleisner1, H. Mansour2, D. Pauly1
1 Sea Around Us, University of British Columbia, Vancouver, V6T 1Z4
2 MERL, Mitsubishi Electric Research Laboratory, 201 Broadway, Cambridge, MA 02139-1955, USA
Background
The large, long-lived fishes at or near the top of marine food webs, when exploited by multispecies fisheries, tend to decline faster than smaller, short-lived fishes with lower trophic levels. This results in the size and mean trophic level of exploited fish assemblages gradually declining, as does the mean trophic level of catches from an ecosystem exploited in this manner.
This phenomenon, now known as ‘Fishing Down Marine Food Webs’ (Pauly et al. 1998a), has been documented through detailed analyses of fisheries catch data from a wide range of ecosystems all over the world (see www.fishingdown.org). The existence of ‘fishing down’ was initially documented globally with FAO landings data from 1950 to 1994, combined with estimates of trophic levels from 60 published trophic mass-balance models from every major aquatic ecosystem type (Christensen and Pauly 1993; Pauly and Christensen 1993, 1995; Christensen 1995).
Since it was first proposed in 1998, the notion that we are ‘fishing down’ in some regions has been corroborated through numerous studies on a large number of marine and freshwater ecosystems (Jackson et al. 2001; Bellwood et al. 2004; Hutchings and Reynolds 2004; Frank et al. 2005; Palomares and Pauly 2005; Scheffer et al. 2005; Morato et al. 2006; Gascuel et al. 2007; Bathal and Pauly 2008; Coll et al. 2010; Pauly 2010; see also www.fishingdown.org).
The widespread occurrence of ‘fishing down’ is the reason why, in 2004, the Convention on Biological Diversity (CBD) chose the mean trophic level of fisheries catches as an index of the biodiversity of large fishes (defined as fish with trophic levels > 3.5), called the Marine Trophic Index or MTI (Pauly and Watson 2005). Since then, several ‘cutoff’ points for MTI, whereby lower trophic level species with high biomass are excluded, have been proposed and used (e.g., Stergiou and Tsikliras 2011; Babouri et al. 2014).
There has been a good deal of debate around the concept of MTI (or cutoff-MTI), in addition to the very idea of ‘fishing down’. This started with Caddy et al. (1998), who accepted the ‘fishing down’ concept, but had what turned out to be minor issues with the FAO fisheries catch data being used demonstrate its occurrence; these issues were addressed in Pauly et al. (1998b).
Only one alternative hypothesis has been proposed to explain observed patterns of mean trophic level declines; thus Essington et al. (2006), while conceding that in the North Atlantic fishing down is an observable phenomenon, suggested that in other regions of the world, changes in trophic level may be better described as ‘fishing through’ the food web, marked by successive addition of lower trophic levels when fisheries focus on this segment of the ecosystem rather than the higher trophic levels. Note, however, that ‘fishing through’ implies that catches in a given area should increase as their mean trophic levels decline.
More recently, Branch et al. (2010) questioned the ability of catch-based MTI to reflect changes in the mean trophic level of the fauna of aquatic ecosystems. However, their study did not consider fishing fleet movements, i.e., the fact that, as fisheries develop, they tend to cover larger areas (notably further offshore), where they encounter less exploited fish communities, whose higher trophic levels mark the decline in MTI in the originally fished area.
Thus, we reiterate here that ‘fishing down’ is best documented with catch time series that pertain to a well-defined area and/or depth range, in which all major species are accessible from the onset. These conditions, which were not stated and not met in the study of Pauly et al. (1998a), was the reason why a number of FAO statistical areas, at the time, did not seem to exhibit ‘fishing down’. Unfortunately, the MTI is often calculated from data pertaining to large areas, e.g., FAO statistical areas, large Exclusive Economic Zones (EEZs), or Large Marine Ecosystems, within which fisheries have expanded over time, with the result that the fishing down effect is partly or completely masked (Bhathal and Pauly 2008). In such cases, the MTI tends to indicate that the overall trophic level is stable or has even increased, while the trophic level of the initially fished region may have in fact declined (Figure 1).
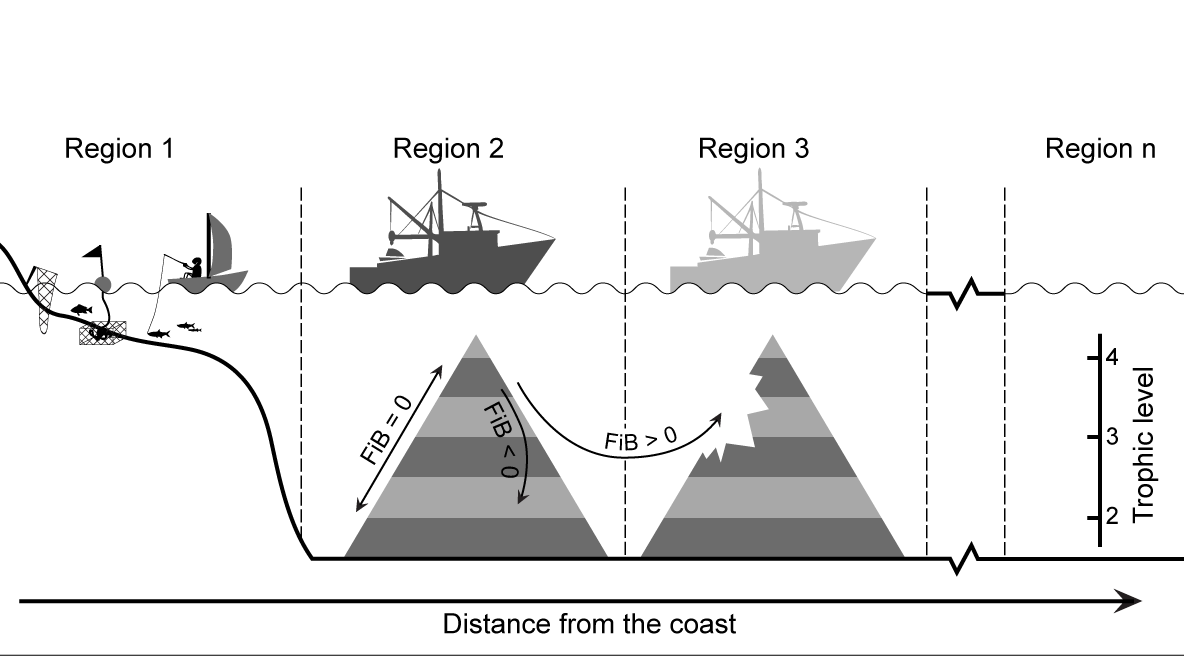
Figure 1. Schematic representation of changes in MTI and FiB index given differing modes of exploitation of coastal resources. At the onset, near-shore small-scale fisheries operate in Region 1, generally exploiting organisms with low trophic levels (invertebrates, small fish, and the juveniles of larger species, yielding a low MTI). At some point, industrial fisheries appear, usually in deeper waters along the coast (in Region 2), and exploit both the demersal and pelagic assemblages, but usually first targeting large, high-trophic level fish. This induces an increase in MTI (if it is calculated as the mean for Region 1 and 2), due to large catches of the higher trophic-level fishes being caught in Region 2, but eventually, the MTI decreases due to their higher vulnerability, relative to that of smaller, lower-trophic level fishes. Increased catch of these lower-TL species compensates for this, and FiB remains at the level to which it was set when the industrial fisheries began (e.g., at zero; see arrow along the left flank of the left trophic pyramid). Alternatively, if effort increases strongly without expansion out of Region 2, biomass may be so reduced that production and hence catches are affected, translating to a declining FiB (inward-turning arrow in left pyramid). Thus, declining catches in Region 2 may induce the fisheries to move into Region 3, which, given the previously untapped resources in that zone, often of higher trophic-level species, will translate into increasing catch and FiB (and possibly in the MTI of the combined Regions 1, 2 and 3, depending on their relative catch levels). This process, which may involve further expansion (to n regions), and completely mask the fishing down effect in coastal zones, can be countered either by analyzing catch time series disaggregated by regions (which are often unavailable), or by using the analytical approach presented in the text.
The Fishing-in-Balance (FiB) index was designed to account for the expansion and contraction of fishing fleets over time as reflected by the trophic level of the catches (Pauly et al. 2000; Bhathal and Pauly 2008; Kleisner and Pauly 2011). Thus, for a given region, the FiB index relates the catches and average trophic level in a given year to the catches and average trophic level in an initial year to determine whether the change in mean trophic level is compatible with the transfer efficiency (TE) of that region. For example, when the TE is 10%, a decline or increase in one trophic level in MTI should correspond to a ten-fold increase or decrease in catches, respectively. A non-zero FiB indicates that the reported catches are higher or lower than what should be compatible with the MTI for that year, and TE of the region.
The trophic level of catches will increase, following an initial decline, if:
(a) the combined effort of the fleet in a given region declines, and shifts such that the biomass of high trophic-level stocks rebuilds, and becomes available to the remaining fishery faster than the low-trophic level stocks;
(b) higher trophic level species migrate into the region;
(c) there have been technological improvements to the fleet, which have increased the catchability of the stock; or
(d) the fishing fleet expands to an adjacent area.
Although the assumptions of fleet and stock stationarity are key to most fish stock assessment models, scenarios (c) and (d) are probable explanations for trophic level increase, especially given that there have been major advances in fleet technology and capacity (e.g., Pauly and Chuenpagdee 2003; Stergiou and Tsikliras 2011), and that there are multiple demonstrations of fisheries expanding geographically and bathymetrically (Morato et al. 2006; Swartz et al. 2010; Watson and Morato 2013). Scenario (c) would occur, for example, if there were an ecosystem where there was only low intensity fishing on certain trophic levels and the fishery was not accessing the entire ecosystem. In this case, the introduction of newer, more efficient technology may provide access to higher trophic levels. If fishing stayed in the same area, fishing down would not be observed until all components of the ecosystem were being harvested. This ‘technical expansion’ would yield similar patterns (e.g., increasing catch and MTI) to a geographic expansion of the fishery.
Regional Marine Trophic Index (RMTI)
Here, we address the issue presented in scenario (d) above, where trophic levels of the catch increase due to fishing in a new location, but cannot resolve scenario (c). Overall, our aim is not to model geographic expansion, but instead to present a correction to MTI for situations where expansion occurs.
Viewed jointly, the MTI and FiB illustrate changes in the average trophic level over time and provide an indication of geographic expansion or contraction over the fishing region. However, it is difficult to evaluate simultaneously the joint message of two graphs representing different aspects of a process (see, e.g., Branch et al. 2010). Therefore, we describe here the recently developed Region-based or ‘Regional’ Marine Trophic Index (RMTI), which combines the properties of both the original MTI and the FiB (Kleisner et al. 2014).
The RMTI is capable of depicting changes in trophic level specific to distinct fishing regions over time. Moreover, unlike the FiB, which is calculated based on an initial pair of catch and MTI over the entire time series, the RMTI is calculated from a potential range of initial MTIs based on the reported catches, which are then aggregated to detect an imbalance between the catches and mean trophic level, given a value of TE. This removes the dependence on a single initial MTI to determine a ‘fishing imbalance’, pinpointing instead the times at which an expansion or contraction of the fishing fleet occurred.
In August 2023, the routines that generate the graphs in this page were improved. Thus, users can now choose the lowest trophic level that is to be considered in the MTI, RMTI and FiB computations, which will allow users to eliminate the effects of strongly fluctuating, large biomass of low-trophic level fish, e.g., sardine or anchovy.
Conceptualization and definition of RMTI
To explain the derivation of the RMTI, a new parameter called ‘potential catch’ is introduced. The potential catch maintains a constant FiB given a reported MTI; put differently, the potential is the maximum possible level of catch that can be obtained when fishing is restricted to a single region, subject to a constant transfer efficiency between trophic levels. This potential catch is derived based on the annually reported mean trophic level considering all possible values of trophic levels within the time series. When, in an annual time series of catches, there exists a year with a total catch that exceeds the potential catch, we consider this year to be the start of the expansion (hereafter referred to as a ‘node’). For the nodal year and each subsequent year, we assume (1) that the maximum catch in the initial region is equal to the potential catch, and (2) that the difference between the potential and the realized catch is assumed to be equal to the catches taken in the new region. This is important, as it allows the resolution of the MTI in an initial region, and the definition of a new MTI time series for the new region.
Consequently, once a node is identified, the MTI in the initial region is defined as the MTI that maintains a FiB equal to zero given the realized catches. Therefore, the MTI time series in the first region is continuous throughout the catch time series and a new MTI time series begins in the first expansion year. Consequently, we can compute an estimated MTI for the new region, using the realized MTI, the realized catches, the estimated catches for the new region, the estimated MTI in the initial region, and an assumption about the TE. This process can be repeated to detect multiple expansion periods by calculating a new potential catch for each new region.
Defining the original MTI and FiB
Let Yik be the reported catches in year k of all species i with trophic level TLi. The MTI in year k is then defined as:
(1)
Given a transfer efficiency TE, we can determine the Fishing-in-Balance index by evaluating the expression of Bhathal and Pauly (2008):
(2)
where Y0 and MTI0 are the realized catches and mean trophic level in the initial year, respectively.
A fishery is said to be fishing in balance when FiBk remains equal to zero, i.e., the catch increases in a predicable fashion when the mean trophic level declines, and vice-versa (illustrated by the arrow parallel to the side of the first pyramid in Figure 1). On the other hand, when FiBk > 0, this implies a scenario in (a) through (d) above, with (d) being the most likely, i.e., that the fishery has expanded geographically (as illustrated by the arrow transiting from the first to the second pyramid in Figure 1). Thus, we shall assume that, given an initial catch Y0 and initial mean trophic level MTI0, when:
(3)
the fishery is in an expansion phase.
Detection of expansion in fisheries
We define the quantity on the right hand side of the above inequality to be the MTI in the initial region (MTI*) when FiBk = 0 and given the reported catch:
(4)
Therefore, we assume that any reported catches:
are indicative of an imbalance in the fishery.
Importantly, the FiB index relies on MTI0 actually reflecting the mean trophic levels of the species available in the (initial) fishing region. However, it is possible that the fleet at the start of the time series did not exploit the full spectrum of available species, which would result in an MTI that does not reflect the species assemblage of the ecosystem under study. This clearly was the case, e.g., in the Gulf of Thailand, where, before the onset of the trawl fishery in the early 1960s, the bulk of the catch consisted of low-trophic level intertidal invertebrates (bivalves, shrimps) and trap-caught small fishes. Then, the mean trophic level of the catch went up for a few years as the newly introduced trawl fishery ramped up, before it strongly declined in the next two decades, as the trawl fishery reduced the fish and invertebrate biomass of the Gulf of Thailand to a small fraction of its original value, while profoundly altering its composition (Pauly and Chuenpagdee 2003).
To remedy this dependence on a single initial MTI, we assume that the initial MTI can be anywhere within the range [TLlower, TLupper] where TLlower and TLupper are the lowest and highest reported trophic levels in the data. By partitioning the range [TL_lower,TL_upper ] into a uniform grid of j trophic levels, we can compute the maximum potential catch (pYkj) per initial trophic level (TLj) where the index j spans the range{1,⋯J}:
(5)
that maintains FiBk = 0 for every year k given the initial catch Y0 and an initial trophic level TLj. We then average the pYkj values for each TLj aggregating them into a maximum potential catch per year (pYk) as follows:
(6)
where Pr(TLj) is the probability that MTI0 = TLj. Here, we use a uniform probability distribution. However, if additional knowledge is available about the structure of the distribution of trophic levels in a given ecosystem, one could apply that probability distribution. The term pYk reflects the expected value of the maximum potential catch that a fishing fleet should be able to extract from a single fishing region, given the transfer efficiency. The expectation is evaluated over the probability distribution of initial trophic levels.
The potential catch pYk is also independent of the initial year’s MTI, thus providing an indicator for the balance of the fishery irrespective of the stationarity of the fleet or the stocks. So long as the realized catches Yk are smaller than pYk, it is unlikely that the fishing fleet has expanded into a new fishing region. On the other hand, if the realized catches Yk exceed the potential catch pYk, then the year indexed by k is likely to be an expansion year or node, indexed by nr, where r refers to each new region identified. Consequently, the reported MTI for every year that follows the node no longer represents the same fishing region, but is now skewed by the catches from the region into which the fleet has expanded. In what follows, we assume that Yk > pYk and demonstrate how to estimate a region-based MTI for each individual region.
Estimation of Region-based MTIs (RMTI)
The detection of the nodes that mark years of expansion allows us to recalculate the corresponding MTIs for every expansion region separately. Our estimation is based on two assumptions: (1) that the fish stocks in the initial region continue to be fished following the year of expansion, and (2) that fishing in the initial region continues to be in balance or contracting given the transfer efficiency of that region.
We define the node of an expansion region (r) as the year prior to which the potential catch becomes larger than the realized catch, i.e.
(7)
To estimate the catches and associated MTIs for all expansion regions (r) in the years (k) that follow the node (nr), we start by estimating the catches from the first region by computing the maximum potential catch, initialized by the realized catches and mean trophic level at the node. In other words, we set FiB = 0 and used the realized MTI (MTIk) to solve for . Hence, we have:
(8)
We then assign the difference between the reported catches Yk in every year k following the node and the estimated to be the catches from the new fishing region:
(9)
Next, we estimate the mean trophic level in the initial region initialized at the node by also setting FiB = 0 and using the reported catch (Yk), yielding:
(10)
The effect of assigning and to the first region ensures that the resulting FiB will remain less than or equal to zero in all years after the node, thereby excluding any further expansion in that region. Additionally, the estimated MTI is predisposed to decrease in the first region after the node. This assumption is likely justified due to the fact that it will usually be more profitable to fish inshore due to lower transit time and costs (e.g., fuel). Based on this assumption, one would expect that the catch-per-unit-effort (CPUE) nearer to the coast would be lower and that, unless inshore fisheries are allowed to rebuild, the mean trophic level would continue to decline. ‘Gravity models’ (Walters and Bonfil 1999; Gelchu and Pauly 2007; Watson et al. 2013), which account for the distribution of CPUE given the cost of fishing, illustrate this concept nicely.
Finally, we estimate the MTI in the second region , noting from the definition of MTI that:
(11)
where ∈ indicates an element in a set of indices, and R1 and R2 are the sets of indices belonging to regions one and two, respectively. From the above equality we can see that the MTI to be estimated in region 2 is given by:
(12)
We then proceed with the same methodology comparing with pYk to detect subsequent nodes.
An important feature of the method described here (RMTI) is that when catches and MTI in the second or subsequent region decrease simultaneously, we assume that there is a contraction in the fishery and we do not continue to assign MTI values in the newly identified region. This results in a break in the RMTI in the new region until the reported catch again exceeds the potential catch. This is a conservative feature of the RMTI in that we try to maintain the lowest number of regions that explain the data.
This approach rests on the premise that fishing in a new region, after the identification of a node year, represents full exploitation of all trophic levels in the ecosystem. Therefore, for every year following the node year, there can only be ‘fishing down’ happening in the first region. Hence, the FiB in the first region following the node year should be less than or equal to zero. Ideally, we would like to maintain a FiB = 0 in the first region after the node. However, solving for both catch and MTI while setting FiB = 0 (Eq. 2) is an ill-posed problem since we would need to solve for two unknowns and we do not possess additional information relating the catch and MTI in the first region. Therefore, we opt for the relaxed condition of FiB less than or equal to 0, which our framework achieves.
Example of RMTI application: India
India is a country for which a geographic expansion of fisheries within the EEZ has been established (Bhathal and Pauly 2008). For India, the new method generates three distinct time series of mean trophic levels, corresponding to three successive regions likely to be parallel along the coast (Figure 2). The first region (Figure 2, lower line, corresponding to the nearshore region), documents a fairly significant decline in trophic levels (from approximately 3.5 to 3.0), which is not apparent in the original MTI, based on the total catch time series. In 1970, a second time series appears in a second region, which reflects strong increases in catches and an increasing FiB. A third region is identified, beginning in the late 1970s/early 1980s, which is associated with a weaker decline in trophic levels, presumably due to the absence, at the edge of the EEZ, of exploitable stocks of low-trophic level fishes. These expansions correspond to the promotion of ‘deep-sea fishing’ in India’s successive Five Year Plans (ICAR 1998; Bhathal 2005). Indeed, each subsequent trend is of a higher average trophic level, indicating that fishing in the new (offshore) regions is based on higher trophic level fish such as tunas, sharks, and billfish.

Figure 2. Illustration of the Region-based MTI (RMTI) for the Indian mainland (i.e., excluding the Andaman and Nicobar Islands). Top panels show catch from 1950-2006 and the FiB index. Bottom panels show the original MTI (c) and the RMTI with three regions identified (d), presumably parallel to the coast, with the longest time series exhibiting the lowest TL values, and the shortest pertaining to offshore taxa (adapted from Kleisner et al. 2014).
Conclusion
Note, finally, that although less straightforward to compute than the original MTI, the RMTI[1] has the key advantage over the MTI that it is less susceptible to biasing by geographic expansion of the fisheries. Additionally, it explicitly accounts for such expansion by producing time series of mean trophic level for different periods and regions within a given area, documenting both the occurrence and the impact of geographic expansion on the trophic structure of marine ecosystems. Also, and most importantly, in regions where there is no expansion, or where there is possibly a contraction of the fisheries, the RMTI for that region shows a break in the time series. Thus, the RMTI does not generate ‘fishing down’ where it does not occur.
The contribution of Kleisner et al. (2014), from which this text was adapted, should be consulted for more details on, and caveats about, this method.
References
Babouri K, Pennino MG, Bellido JM (2014) A trophic indicator toolbox for implementing an ecosystem approach in data-poor fisheries: the Algerian and Bou-Ismael Bay example. Scientia Marina 78: 37-51.
Bellwood DR, Hughes TP, Folke C, Nystrom M (2004) Confronting the coral reef crisis. Nature 429: 827-833.
Bhathal B (ed) (2005) Historical reconstruction of Indian marine fisheries catches, 1950-2000, as a basis for testing the “Marine Trophic Index.” Fisheries Centre Research Reports 13(5), University of British Columbia, Vancouver, Canada. 122 p.
Bhathal B, Pauly D (2008) ‘Fishing down marine food webs’ and spatial expansion of coastal fisheries in India, 1950-2000. Fisheries Research 91: 26-34.
Branch TA, Watson R, Fulton EA, Jennings S, McGilliard CR, Pablico GT, Ricard D, Tracey SR (2010) The trophic fingerprint of marine fisheries. Nature 468: 431-435.
Caddy JF, Csirke J, Garcia SM, Grainger RJR (1998) How pervasive is “fishing down marine food webs?”. Science 282: 1383.
Christensen V, Pauly D (1993) Trophic models of aquatic ecosystems, Vol 26. ICLARM Conference Proceedings, Manila, Philippines.
Coll M, Piroddi C, Steenbeek J, Kaschner K, Ben Rais Lasram F, Aguzzi J, Ballesteros E, Bianchi CN, Corbera J, Dailianis T, Danovaro R, Estrada M, Froglia C, Galil BS, Gasol JM, Gertwagen R, Gil J, Guilhaumon F, Kesner-Reyes K, Kitsos MS, Koukouras A, Lampadariou N, Laxamana E, Lopez-Fe de la Cuadra CM, Lotze HK, Martin D, Mouillot D, Oro D, Raicevich S, Rius-Barile J, Saiz-Salinas JI, San Vicente C, Somot S, Templado J, Turon X, Vafidis D, Villanueva R, Voultsiadou E (2010) The biodiversity of the Mediterranean Sea: estimates, patterns, and threats. Plos One 5: e11842.
Essington TE, Beaudreau AH, Wiedenmann J (2006) Fishing through marine food webs. Proceedings of the National Academy of Science 103: 3171-3175.
Frank KT, Petrie B, Choi JS, Leggett WC (2005) Trophic cascades in a formerly cod-dominated ecosystem. Science 308: 1621-1623.
Froese R, Kesner-Reyes K (2002) Impact of fishing on the abundance of marine species. ICES CM 2002/L: 12, Copenhagen, Denmark.
Gascuel D, Labrosse P, Meissa B, Taleb Sidi MO, Guénette S (2007) Decline of demersal resources in North-West Africa: an analysis of Mauritanian trawl-survey data over the past 25 years. African Journal of Marine Science 29: 331-345.
Gelchu A, Pauly D (2007) Growth and distribution of port-based global fishing effort within countries’ EEZs from 1970 to 1995. Fisheries Centre Research Reports 15(4), University of British Columbia, Vancouver. 99 p.
Hutchings JA, Reynolds JD (2004) Marine fish population collapses: consequences for recovery and extinction risk. Bioscience 54: 297-309.
ICAR (1998) Vision-2020 CMFRI perspective Plan. Indian Council of Agriculture Research, New Delhi.
Jackson BC, Kirby MX, Berger WH, Bjorndal KA, Botsford LW, Bourque BJ, Bradbury RH, Cooke R, Erlandson J, Estes JA, Hughes TP, Kidwell S, Lange CB, Lenihan HS, Pandolfi JM, Peterson CH, Steneck RS, Tegner MJ, Warner RR (2001) Historical overfishing and the recent collapse of coastal ecosystems. Ecology 84: 162-173.
Kleisner K and Pauly D (2011) The Marine Trophic Index (MTI), the Fishing in Balance (FiB) Index and the spatial expansion of fisheries. pp. 41-44 In: Christensen V, Lai S, Palomares MLD, Zeller D and Pauly D (eds.), The State of Biodiversity and Fisheries in Regional Seas. Fisheries Centre Research Reports 19(3), University of British Columbia, Vancouver.
Kleisner K, Mansour H and Pauly D (2014) Region-based MTI: resolving geographic expansion in the Marine Trophic Index. Marine Ecology Progress Series 512: 185-199.
Morato T, Watson R, Pitcher TJ, Pauly D (2006) Fishing down the deep. Fish and Fisheries 7: 23-33.
Pauly D (2010) Five Easy Pieces: The Impact of Fisheries on Marine Ecosystems. Island Press, Washington, DC. xii + 193 p.
Pauly D, Christensen V (1993) Stratified models of large marine ecosystems: a general approach and an application to the South China Sea. In: Sherman K, Alexander LM, Gold BD (eds) Large Marine Ecosystems: Stress, Mitigation and Sustainability. AAAS Press, Washington, DC.
Pauly D, Christensen V (1995) Primary production required to sustain global fisheries. Nature 374: 255-257.
Pauly D, Christensen V, Dalsgaard J, Froese R, Torres Jr. F (1998a) Fishing down marine food webs. Science 279: 860-863.
Pauly D, Christensen V, Walters C (2000) Ecopath, Ecosim, and Ecospace as tools for evaluating ecosystem impacts of fisheries. ICES Journal of Marine Science 57: 697-706.
Pauly D, Chuenpagdee R (2003) Development of fisheries in the Gulf of Thailand Large Marine Ecosystem: Analysis of an unplanned experiment. In: Hempel G, Sherman K (eds) Large Marine Ecosystems of the World 12: Change and Sustainability. Elsevier Science, Amsterdam.
Pauly D, Froese R, Christensen V (1998b) How pervasive is “Fishing down marine food webs”: response to Caddy et al. Science 282: 183.
Pauly D, Palomares M (2005) Fishing down marine food webs: It is far more pervasive than we thought. Bulletin of Maritime Science 76: 197-211.
Pauly D, Watson R (2005) Background and interpretation of the “Marine Trophic Index” as a measure of biodiversity. Philosophical Transactions of the Royal Society-Biological Sciences 360: 415-423.
Scheffer M, Carpenter S, de Young B (2005) Cascading effects of overfishing marine systems. Trends in Ecology and Evolution 20: 579-581.
Stergiou KI, Tsikliras AC (2011) Fishing down, fishing through and fishing up: fundamental process versus technical details. Marine Ecological Progress Series 441: 295-301.
Swartz W, Sala E, Tracey S, Watson R, Pauly D (2010) The spatial expansion and ecological footprint of fisheries (1950 to present). Plos One 5 (12): e15143.
Walters CJ, Bonfil R (1999) Multispecies spatial assessment models for the British Columbia groundfish trawl fishery. Canadian Journal of Fisheries and Aquatic Science 56: 601-628.
Watson R, Cheung WWL, Anticamara JA, Sumaila UR, Zeller D, Pauly D (2013) Global marine yield halved as fishing intensity redoubles. Fish and Fisheries 14(4): 493-503.
Watson RA, Morato T (2013) Fishing down the deep: accounting for within-species changes in depth of fishing. Fisheries Research 140: 63-65.
[1] The R-code for running the RMTI and sample data are available on the Regional MTI tools page.

